További Tudomány cikkek
-
 Fidrich Róbert: Az Európai Bizottság javaslata teljesen tudománytalan
Fidrich Róbert: Az Európai Bizottság javaslata teljesen tudománytalan - Elnyeli a föld a kínai nagyvárosokat
- Az őskorallok minden élőlénynél előbb világítottak az óceánok mélyén
- Meglepő dolgok derültek ki az Alzheimer-kór okairól egy új kutatásból
- A légszennyezés lelassítja a kisgyerekek agyfejlődését
Sosem voltam jó matekból. Valamikor az alsó és felső tagozat határán az agyam úgy döntött, hogy én bizony nem vagyok reálos. Nekem ez nem megy, és ez látszott is a teljesítményemen, tanáraim minden igyekezete ellenére. A kockás négyzetrácsos füzetet elborító számsorok csak arra jók, hogy stresszeljenek: bele sem férek a rubrikába, és amúgy is, valahol biztos elszámolom majd. Nem segített sokat az sem, hogy vonalzóval is képtelen voltam egyenes vonalat húzni (ez azóta sem változott). Amúgy is, minek, hiszen ma már ott az internet, a mindent tudó Google, és pár éve már velünk van a matekra és reál tudományokra specializálódott Wolfram Alpha is.
Míg mások zárt szobában, számológéppel (szigorúan olyannal, amely szöveges értékek tárolására és megjelenítésére nem alkalmas) és függvénytáblázattal felvértezve, de számítógép és internet nélkül próbálkoztak, én egészen rendhagyó módon írtam meg újra a matekérettségit az igazi után jó pár évvel. A tavalyi feladatsorral küzdöttem meg az idei érettségi előtt egy nappal.
Józan paraszti Google-lel
A következő szabályokat állítottam fel a fiktív, de annál igazságosabb matekérettségimen:
- Bármit használhatok, amit számítógépről, internettel elérek.
- De nem kérdezek meg másokat személyesen, telefonon vagy cseten.
- Úgy csinálok, mintha egy képletre, megoldási sablonra sem emlékeznék (ez nem lesz nehéz), minden ilyesmit a netről szerzek be.
- Időlimitem nincs, de ha megakadok, megyek tovább, nem töltök órákat egy feladattal.
- Ami fejből, gondolkodás és interbet nélkül is nélkül megy, azt azért megoldom.
- Nem fizetek semmiért, előfizetéses weboldalak kizárva.
Az eredményből persze nem lehet általánosítani: teljesen szubjektív, hogy mi az, ami nekem egyből beugrik, lehet, hogy mások a számítógép segítségével is korábban elakadtak volna, vagy éppen anélkül is könnyedén megoldanak egy feladatot. Mindenesetre régóta foglalkoztatja az érettségizőket, milyen lenne egy olyan feladatsor, amihez bármit használhatunk: egyszerűbb, esetleg semmivel sem könnyebb? Végigküzdöttem a feladatokat, hogy rájöjjek.
1. feladat
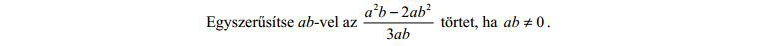
Az első feladat máris tökéletes puding próbája: odáig rendben, hogy van két nagyszerű eszközöm a Google és a Wolfram Alpha képében, de nem tudok beléjük ilyen formában törtet írni. Ráadásul, hogyan magyarázzam meg a programoknak, hogy „egyszerűsítse ab-vel”? A Google-t itt eleve kizártam, maradt az, hogy valahogy bepötyögöm a Wolfram Alphába a törtet.
A hatványozást az Altgr+3 billentyűkombinációval lehet előcsalni, a törtvonalat zárójelezéssel csaltam el, így ez lett a törtből: (a^2-2ab^2)/(3ab). Entert nyomtam, és vártam, hogy megtörténjen a csoda, kapok valami használhatót. Az alternatív formulák (angolul muszáj tudni az ilyen érettségizéshez) között volt olyan, ami nagyon hasonlít a megoldásra, de a feladat megoldását nem kaptam meg, részpontszám pedig nem adható.
Update: persze, jól kellett volna beírni az egyenletet: ((a^2)b-(2ab^2))/(3ab). A tábláról másolás sem ment régen, így úsznak el könnyedén pontok.
0/2 pont
2. feladat

Újra nem sokra megyek digitális tudományommal. Marad a jó öreg Wikipedia, előbbre nem vagyok, a kapott képlet túl általános. Át a térfogat lapra, itt van képlet a hengerhez: π×r2×h. Pi-t már elég a Chrome címsorába beírni, enter nélkül kapom is az értékét, r a sugár jele, ezt még én is tudom, ez lesz a kisebbik oldal, így a képletem: π*5^2*12, amire a Wolfram szépen ki is adja, hogy 300π. Győzelem!
3/3 pont
3. feladat
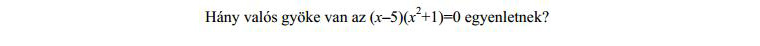
Ez az eddigi legegyszerűbb: az első feladatból már megismert módon átírom az egyenletet a gépi gyomorral is emészthető (x-5)(x^2+1)=0 formára, és WA Real solution részénél már látom is, hogy az eredmény 5. Mást nem ír, úgyhogy egy valós gyök van (a megoldókulcs az x=5 megoldásra csak egy pontot ad). Ehhez persze megint csak tudnom kell angolul, és azt sem árt tudni, hogy mit jelent az hogy az egyenlet gyöke.
2/2 pont
4. feladat
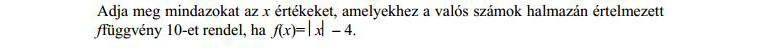
Szerencsém van, ugyanaz a mozdulatsor, mint az előbb. Pár másodpercnél nem kellett több, hogy rájöjjek, az abszolútérték-jelet helyettesíthetem azzal, ha azt írom, abs(x). Ezt gépeltem a Wolframba: 10 = abs(x)-4. Még grafikus ábrázolást is kapunk, ez sokaknak segítség lehet, jól látszik rajta, hogy két megoldás van, és az is, hogy hol. A pontos értéket is megkapjuk: ±14.
2/2 pont
5. feladat

Ezzel a feladattal meg sem próbálkoztam: ha ki is derítem a fent megadott fogalmakat, akkor sem fogom tudni megindokolni a választ. Ezt nem tanulja és csinálja meg helyettem senki.
0/2 pont
6. feladat
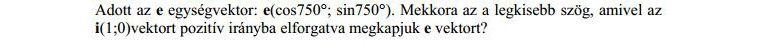
A Wolfram Alpha sok mindent elmond a cosinusról meg a sinusról, gyönyörű rajzokat kapok, elolvashatom a vektor definícióját is, de ezt a feladatot egyszerűen nem tudtam általa értelmezhető módon megadni. Update: Ha jobban ismerném a programot, ez is meglett volna. Bár lassan annyi parancsot tanulok hozzá, hogy egyszerűbb a képleteket.
0/2 pont
7. feladat

Függvény, megint jó eséllyel indulok. A szokásos átírással megadom a gépnek a függvényt. Látok egy szép grafikonábrázolást, sok minden látszik rajta, és azt is látom, hogy a gyöke -9. Pár sorral lejjebb pedig azt is kiírta, hogy a globális minimum -9-nél. Nyertem, de levezetés, indok nincs, ezzel vesztek egy pontot.
1/2 pont
8. feladat

Nagyon meglepődtem, amikor kiderült, hogy a Wolframnak hiába írom be angolul a kérdést, nem tud mit kezdeni vele. Ahogy a Google sem. Meg az Ask.com sem. (érdekes, hogy utóbbi kettő négyjegyűre akarja javítani a kérésem). Elvéreztem.
0/2 pont
9. feladat

Ez az a feladat, amihez semmit nem kell tudni alsós szintű számoláson kívül: kicsit baltával szalonnázás, de ránéztem, a biztonság kedvéért összeadtam a szögeket (jé, 360), ezzel osztottam a 720-t (jé, kettő), majd a megfelelő szögekkel felszoroztam. Ez volt a legolcsóbb három pontom.
3/3 pont
10. feladat
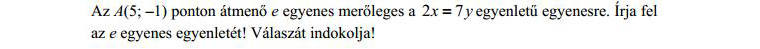
Így már jártam: nem tudom úgy megszövegezni a feladatot, hogy a Google vagy a tudományos kereső értelmezni tudja. Valószínűleg egyébként megoldható, ez inkább az én szegénységi bizonyítványom, mindenesetre mindenképpen több lépésre lenne szükség. (És igen, itt a megoldás.)
0/3 pont
11. feladat

Tökéletes példája annak, hogy a gép még nem ember. Egyszerű feladat, mindössze néhány egymondatos szabályt kell hozzá ismerni, a ma nyilvánosan, pár kattintással elérhető algoritmusok mégsem fogják nekünk megmondani a választ, ahogy azt már láttuk a 8. feladat sokkal egyszerűbb kérdésénél is.
0/4 pont
12. feladat

Ehhez megint nem kellett semmi: 1. =-1, 2.=1, 3.=0, 4.=1, 5.=1, 6.=2, összeadtam (számológép nélkül!), 4, ennyi.
3/3 pont
Az első részben tehát 15 pontot értem el az elérhető 30-ból, ez 50 százalék. (Először 14 pontot számoltam, na, ezért lett négyes az igazi érettségim anno. Többek között.) A matekérettségi viszont két részből áll, a második kevesebb, de összetettebb, hosszabb feladatokat tartalmaz.
MÁSODIK RÉSZ
13. feladat

Csak rá kellett néznem a második rész feladataira, és tudtam, hogy nem sok jóra számíthatok: a szöveges feladatok már az első részben is azt jelentették, hogy nem tudom megérteni a géppel, mit akarok. Fejből nem ment, ugrottam.
0/12 pont
14. feladat
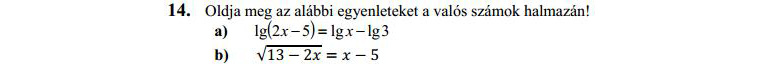
Végre, egyenletek, a gépek kedvencei! Az a feladat megoldása könnyedén megvolt, tényleg csak begépeltem az egyenletet, viszont a levezetést csak a fizetős Wolfram Alpha Pro verzió mutatja meg. Bukta - lenne, de egy alternatív formulát azért kapok ingyen is: lg(x) = lg(6x-15), ebből már még egyet tudok előrelépni (a logaritmusok azonosságára emlékeztem), és szebben kijön, hogy x=3, amit amúgy is megkaptam. A levezetésből hiányzik az indoklás, nyilván nem ér maximum pontot, de így is valami. Az értelmezési tartományokat nem kaptam meg, de a megoldókulcs szerint így is jár 4 pont.
A b feladathoz a gyökvonást kellett az abszolút értékhez hasonlóan beírnom: root(13-2x)=x-5, a megoldás már meg is van, x=6. Hát, egy fenét. Újabb döbbenet: a Wolfram nem jól old meg egy egyszerű másodfokú egyenletet (ugyanis azt kapok, ha tényleg elkezdem megoldani a feladatot). (Update: a root az egyenlet gyöke, így nem jön ki. Amúgy a másodfokúakra van külön eszköz.) Az egyetlen szerencsém, hogy csak valós megoldásokat kérnek, így 1 pont (a többi mind a kifejtésért járna).
5/12 pont
15. feladat

Megint szöveges feladatok, amelyeknél a megoldás folyamata is a szövegben van. A gépek ezt egyelőre angolul sem értik, nemhogy magyarul. Bukta.
0/12 pont
16-18. feladat
Ezek közül a feladatok közül kettőt kell megoldani, mindegyik hosszú szöveges, ahol a gép tudás semmit sem ér. Mindegy melyiket választottam, az eredmény: 0/24 pont.
Végeredmény
Az első részben összesen: 15 pontot szereztem meg az elérhető 30-ból, a második részben összesen 5 pontot értem el a maximális 70-ből. Az összesített végeredmény 20/100, ami még ilyen matekos teljesítménnyel is jól láthatóan 20 százalék.
A kormány ugyanis azóta közép- és emelt szinten is 25 százalékra emelte a ketteshez szükséges eredményt. Bár sokkal több dologra is emlékezhetnék abból, amit sok év alatt megtanultam matekból, az azért jól látszik, hogy a mai digitális eszközök még nem helyettesíthetik a matematikaoktatást, a jó matektanárokat.
Valljuk be, azért a másodfokú egyenletek megoldóképletét egyszer megtanulni nem olyan nagy dolog, márpedig a tudományos kereső ma még elrontja a legegyszerűbbet is. Ráadásul, amikor a program jó eredményt ad, akkor is érteni kell, mit látunk. Az már csak hab a tortán, hogy levezetés csak a fizetős verzióhoz jár. Maga a Google-keresés sem sokat segít, ha valaki pont azt a feladatot nem oldotta már meg előttünk. Ami a Google-lel megvan, azt a függvénytáblázatból is kikereshetjük. Ugyanez igaz a Wikipédiára is, ami sokszor egyszerűen túl bonyolult a középiskolai szinthez.
Összességében az érettségi megoldásában nem sokat segít, hogy bármit használhatunk, hiszen meg is kell érteni a feladatot (ami persze nem azt jelenti, hogy a példa életszerű, vagy hogy valaha még használni fogja az egyszeri érettségiző a most megmért tudását). De bele nem hal senki, és talán a boltban sem verik át. Ha pedig egyszer majd tanítanak alapvető pénzügyi ismereteket az iskolában, alapvető matematikai ismeretekre akkor is szükség lesz.



