A 2017-es matekérettségi megjósolta a járványt?

A matematikaérettségit összeállító bizottság mintha a jövőbe látott volna, amikor a 2017 májusában megírt egyik emelt szintű feladatsort készítette. A feladatoknak akkor nem volt nagy visszhangja, mert csak az a 74 érettségiző kapta meg, akik idegen nyelven vizsgáztak. Azonban a feladatsor 8. feladata megdöbbentően szorosan kapcsolódik jelenlegi élethelyzetünkhöz, három részből áll, és mindegyik rész egy fiktív járvány egy-egy aktuális kérdéséről szól. (A vizsgaleírás szerint a feladatsor 30-40%-ban „a hétköznapi élethelyzetekhez kapcsolódó” szöveges feladatokat tartalmaz.)

Az üzenet világos: még ha csak 2 ezrelék is a város lakosságának átfertőzöttsége, akkor is 15% a valószínűsége annak, hogy egy tele buszon találunk egy fertőzöttet. Azaz még alacsony átfertőzöttség esetén sem engedhető meg, hogy a tömegközlekedési járművek zsúfoltak legyenek: még ha kevés az utas, akkor is fenn kell tartani a munkanapi járatsűrűséget.

A tanulság: még ha a járvány terjedése eleinte lassúnak is tűnik, tehát a napi esetszám-növekedés csak 5%, egy hónap alatt akkor is megötszöröződik a fertőzöttek száma. A feladathoz hasonlóan a legtöbb országban a fertőzések növekedési üteme eleinte exponenciális volt. Az exponenciális függvény sajátossága, hogy a kezdeti lassúnak tűnő növekedés hirtelen nagyon fel tud gyorsulni.

A legérdekesebb, egyben a legmegdöbbentőbb következtetésekkel a feladat harmadik része szolgál:

Az eredmény szinte hihetetlen: a teszt 99%-os pontosságot ígér a fertőzés kimutatásában (és téves pozitív jelzést is csak az esetek 4%-ában ad), egy pozitív teszteredmény esetén mégis 5%-nál kisebb valószínűséggel lesz fertőzött a tesztalany. Hogyan lehetséges ez? Nézzük meg a részleteket!

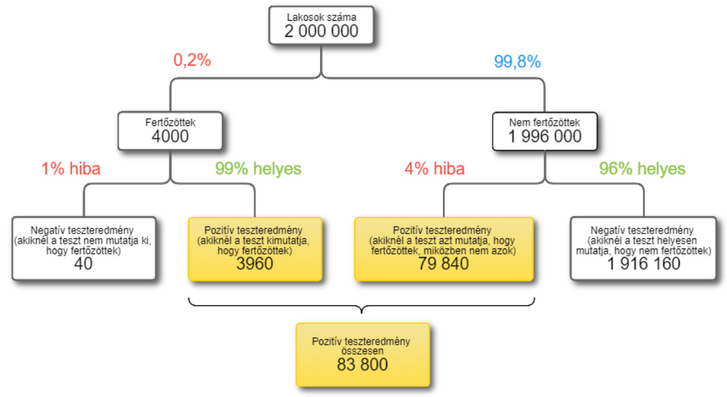
Tegyük fel, hogy a városban 2 millióan laknak. A szöveg szerint a lakosság 0,2%-a, tehát 4000 ember fertőzött, a többi 1 996 000 ember nem fertőzött. Ha mindenkit tesztelnénk, a 4000 fertőzött 99%-ánál, tehát 3960 embernél (helyesen) kimutatná a teszt a fertőzöttséget. Ugyanakkor az egészséges lakosok 4%-ánál, tehát 79 840 embernél is (tévesen) pozitív eredményt mutatna a teszt. Lesz tehát összesen (3960 + 79 840 =) 83 800 pozitív tesztünk, de közülük csak 3960 ember beteg ténylegesen. Azaz pozitív teszteredmény esetén a tényleges fertőzöttség valószínűsége csak 3960 / 83 300, ami kb. 4,73%, tehát valóban kevesebb 5%-nál.

Akkor ez hibás teszt, és érdemes a kukába dobni?

Nem érdemes. Ahogy a szöveg is mondja, a gyorsteszt nem a fertőzöttség megbízható kimutatására való. De akkor mire? Például arra, hogy valakiről kimutassa, hogy nem fertőzött. A fentihez hasonló gondolatmenettel ugyanis azt kapjuk, hogy negatív teszteredmény esetén tesztalanyunk közel 99,998% valószínűséggel valóban egészséges.

Azért is kaptunk 5% alatti értéket pozitív eredmény esetén a tényleges fertőzöttségre, mert a feladatban a teljes lakosságon belül nagyon alacsony a fertőzöttek aránya. Így a sok egészséges ember közt előforduló 4%-nyi téves pozitív teszteredmény jóval nagyobb esetszámot (79 840) jelent, mint a kevés beteg közötti 99%-nyi valós (3960). Ha a lakosság átfertőzöttsége 20% lenne, akkor mindjárt változna a helyzet: a pozitív eredményt produkálók már 38% valószínűséggel lennének ténylegesen betegek.

Ha 5%-ban betegek csak a pozitív teszteredményt produkálók, akkor hogy lehet megtalálni a ténylegesen betegeket? Ahogy a feladat szövegében is szerepelt, ez egy gyorsteszt, ami alkalmas például előszűrésre. A pozitív eseteket érdemes egy második, vélhetően drágább, de ebben az irányban pontosabb eszközzel újratesztelni. De ha ilyenünk nincs, akkor a gyorsteszt másodszori alkalmazása is szóba jöhet: ha csak az első körben pozitív 83 800 esetet teszteljük újra, akkor a második tesztelésen is pozitívnak bizonyulók már 55% eséllyel tényleg fertőzöttek. (Ez persze csak akkor igaz, ha a téves pozitív riasztásokat valóban a véletlen, és nem valamilyen szisztematikus hiba, például a tesztalany szervezetében jelenlevő valamilyen anyag okozta.)

Egy teszt pontosságát nehéz egyetlen számmal leírni. A teszt két irányban is tévedhet: pozitív esetet mutathat negatívnak, vagy negatívat pozitívnak. A feladatbeli teszt megbízhatósága az első szempontból 99%-os, a második szempontból pedig 96%-os, mégis könnyű lett volna lejárató cikket írni róla azzal a szalagcímmel, hogy a teszt pozitív eredménye az esetek 95%-ában téves.

Amikor azt olvassuk, hogy „egy teszt megbízhatósága 30 százalék”, nem világos, hogy ezt hogy kell érteni: 30 százalékban mutat pozitív eseteket negatívnak? Vagy negatívokat pozitívnak? Esetleg az összes teszteredmény 30 százaléka helyes? (Ez utóbbi esetben egyébként a teszt remekül használható lenne: egyszerűen a kimutatott eredmény ellenkezőjére kellene következtetni, és máris egy 70%-os megbízhatóságú tesztet kapnánk.) A feladatban szereplő teszt az esetek 96,01%-ában ad helyes eredményt, de ez az érték függ a lakosság átfertőzöttségétől, tehát nem egy állandó adat.

Ennél biztosan lehet jobb tesztet készíteni, ugye?

Ez először is attól függ, mit nevezünk jó tesztnek, egyáltalán mire készítjük a tesztet: inkább a pozitív eseteket kívánjuk megfogni, vagy a negatívokat? Ha például nem fertőzöttek, hanem űrhajósok kiválasztására készítünk tesztet, akkor inkább elfogadjuk, hogy a teszt egy alkalmas (pozitív) jelöltet elutasítson, mint hogy egy alkalmatlant elfogadjon. Ráadásul, ha az egyik irányban javítjuk egy teszt megbízhatóságát, az gyakran azt eredményezi, hogy a másik irányban romlani fog. Választanunk kell, hogy melyik a fontosabb. Nyilván a legkényelmesebb az lenne, ha a teszt mindkét irányban nagyon erős lenne, de egy ilyen teszt kifejlesztése és használata biztosan időben és pénzben is nagyon sok ráfordítást igényel, ezért valószínűleg nem éri meg.

Amikor egy járványban szeretnénk kiszűrni a betegeket, az a fontosabb, hogy pozitív eseteket ne mutasson a teszt negatívnak: kisebb baj származik ugyanis abból, ha egy egészséges embert vizsgálni kezdenek, mint ha egy fertőzöttet visszaengednek a társadalomba. A feladatbeli teszt is így viselkedik: a fertőzöttséget nagyobb biztonsággal mutatja ki, mint a nem-fertőzöttséget. A fertőzöttség 99%-os kimutatása bőven belül van az elfogadható hibahatáron. Azonban ha egy teszt a fertőzötteknek csak a harmadát jelzi, míg az egészségesek 10%-ánál fals pozitív jelzést ad, a feladatbeli szituációban a pozitív tesztalanyoknak kevesebb, mint 0,7%-a lenne ténylegesen beteg. A legnagyobb baj természetesen az, hogy ez a teszt a betegek jelentős részét egészségesnek mutatja.

Figyelemre méltó, hogy a matematikaérettségi vizsga egy feladata mennyire fontos és releváns kérdések vizsgálatát várt el a diákoktól (amikről akkor még nem is tudhattuk, hogy három év múlva mennyire fontosak és relevánsak lesznek). Csak azt sajnálhatjuk, hogy a feladatnak nem volt egy negyedik része, amiből azt is megtudhatnánk, hogy meddig kell még együtt élnünk a járvánnyal.

(A cikk szerzői Csapodi Csaba, az ELTE TTK Matematikai Intézetének munkatársa, és Koncz Levente, az Óbudai Árpád Gimnázium matematikatanára.)

(Borítókép: Koronavírus-járvány miatt arcmaszkot viselő járókelők Salgótarján városában 2020. május 4-én. Fotó: Bődey János / Index)