Az igazi különbség a 30-as és az 50-es sebesség között

Az alábbiakban arra a kérdésre adok választ, hogy milyen különbséget jelent az, ha egy autó 30 km/h helyett 50 km/h sebességről fékez valamilyen veszélyes helyzetben. Ehhez kénytelen leszek matematikai eszközöket bevetni, de igyekszem érthetően fogalmazni.

Tekintsük a következő helyzetet:

Egy kertvárosi övezetben, ahol 30 km/óra a megengedett legnagyobb sebesség, egy autó 30 km/óra sebességgel halad. Megelőzi őt egy másik autó 50 km/óra sebességgel. Egymás mellett haladnak, amikor előttük egy gyerek kiszalad az úttestre egy elgurult labdáért. A két autó sofőrje egyszerre kezd fékezni, és a két autónak ugyanolyan erős fékjei vannak. A lassabb autó éppen megáll a gyerekek előtt. Mekkora „megmaradó” sebességgel halad ugyanitt a gyorsabb autó?

A kérdést kicsit átfogalmazva: ha 30 km/h sebesség esetén éppen meg tudok állni egy adott ponton, akkor mennyi lenne a sebességem ugyanitt, ha 50 km/h sebességről kezdtem volna ugyanúgy fékezni? Még élesebben fogalmazva: mekkora sebességgel (nevezzük ezt megmaradó sebességnek) ütném el az … útra kiguruló labdát, ha 30 helyett 50-nel hajtanék?

Azt kérem az olvasótól, hogy most tippelje meg: mekkora lehet ez a megmaradó sebesség, ha 30 helyett 50 km/h-val haladunk?

Többen talán 20 km/h körüli sebességre tippelnek. Ez nem a helyes válasz, pontosabban: ez egy helyes válasz, de nem a kitűzött kérdésre. Ez arra a kérdésre a helyes válasz, hogy akkor, amikor a 30 km/h sebességről fékező autó megáll, akkor mekkora sebességgel halad az 50 km/h sebességről fékező autó. A mi kérdésünk pedig arra vonatkozik, hogy ott, ahol a lassabb autó megáll, ott mekkora sebességgel halad a nagyobb sebességről fékező autó.

A kérdés megválaszolásához egy olyan függvényre van szükségünk, amely a fékezés során megtett út függvényében adja meg a lassuló autó sebességét. Érthetőbben fogalmazva: azt kell tudnunk, hogy az autó sebessége hogyan változik a fékút során.

Ezt a függvényt most egy olyan grafikonon ábrázoljuk, ahol a vízszintes tengelyen a fékezés megkezdésétől számított utat jelöljük méterben, a függőleges tengelyen pedig az autó sebességét jelöljük km/h-ban. A függvény alakját természetesen befolyásolja a lassulás mértéke (az alábbi ábrákon ennek egy tipikusnak tekinthető értéket adtunk, ami persze függ az útviszonyoktól vagy a fékek állapotától), de az az érdekes, hogy az eredeti kérdésre adandó választ ez az érték nem befolyásolja.

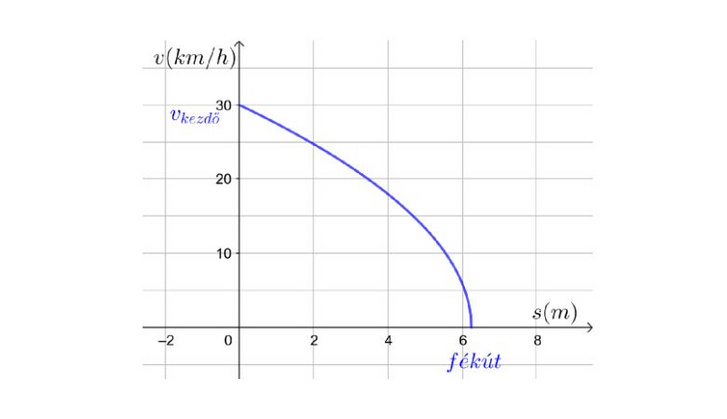
A grafikonról leolvasható (és persze ki is számítható), hogy a fenti adatok esetén kb. 6,2 méter lesz autó fékútja, ennyi kell ahhoz, hogy a fékezés kezdetétől megálljon.

Hogy mi ezen a grafikonon az érdekes? Nézzük meg, hogy 30 km/h sebességről lassuló autó mekkora utat tesz meg, amíg a sebessége a felére csökken:

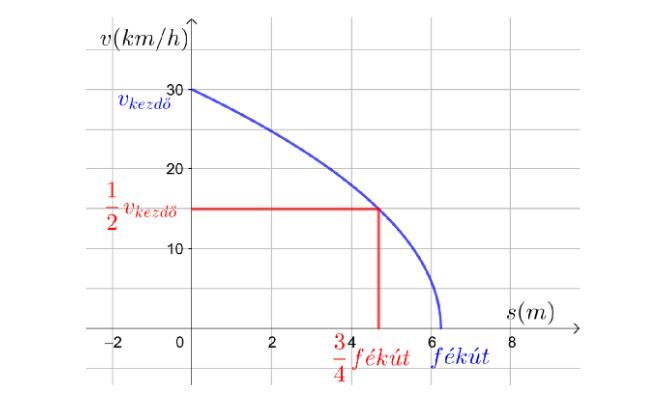
Ez lesz a meglepő válasz kulcsa:

A féktáv háromnegyed részén csökken felére a sebesség, majd a féktáv utolsó egynegyed részén veszíti el a sebesség másik felét.

Most már közel vagyunk ahhoz, hogy megválaszoljuk az eredeti kérdést. Tudjuk, hogy a lassabb autónak kb. 6,2 méter kellett ahhoz, hogy megálljon, a kiguruló labdától tehát ilyen távolságra kezdi meg mindkét autó a fékezést. Most már csak azt kell tudnunk, hogy az 50 km/h-s sebességről fékező autó sebessége mennyire csökken 6,2 méter alatt. Nézzük meg közös ábrán a 30-ról és 50-ről csökkenő lassulás grafikonját.

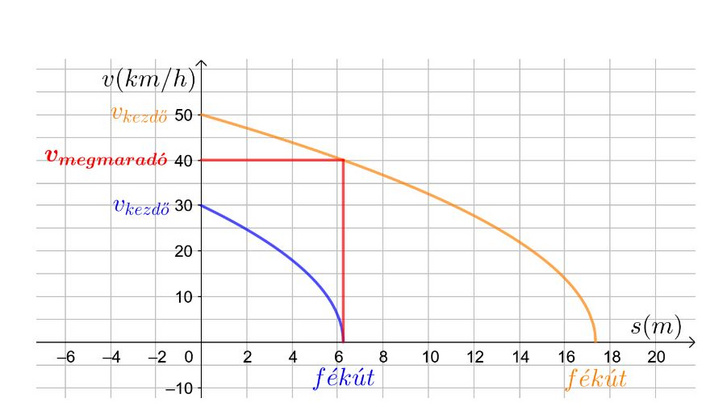
Jól látható, hogy az 50 km/h-ról lassító autó sebessége 40 km/h-ra csökkent ez alatt az út alatt.

(A fenti ábrán az is jól látszik, hogy a fékezés elején fennálló kb. 1,7-szeres kezdősebesség, majdnem 3-szoros féktávot eredményez.)

Most tegye fel a kezét, aki ennyit tippelt!

Jó, köszönjük, letehetik. A helyzet az, hogy a valóságban még ennél is nagyobb lesz a megmaradó sebesség!

A fenti okfejtés során ugyanis eltekintettünk a sofőrök reakcióidejétől. Legyen ez mindkét sofőr esetén mondjuk 1,2 másodperc. A labda megpillantása után 1,2 másodperccel a gyorsabb autó már kb. 16,7 métert megtesz, mikor elkezd fékezni, a lassabb autó viszont csak 10-et. Tehát a nagyobb sebességről fékező autó kb. 6,7 méterrel közelebb van a kiguruló labdához, amikor elkezd fékezni, ennyivel el kellene tolni a narancssárga grafikont „jobbra”. Viszont ezen a 6,7 méteren a lassabb autó meg is tud állni, láttuk, hogy az ő féktávja csak 6,2 méter!

A pontos – és elég meglepő – válasz tehát a kérdésre:

Ennek ismeretében érdemes mindenkinek megfontolnia, hogy milyen következményei lehetnek a nagyobb sebességgel közlekedésnek.

Csapodi Csaba matematikus, Eszterházy Károly Egyetem, Eger

Ezzel az írással az Index folytatja társadalmi vitasorozatát a témában, ahová várjuk a pro és kontra véleményeket. Eddigi cikkek a vitában:

• Kürti Gábor (Kerékpárosklub): Életünket vagy kényelmünket védjék a sebességhatárok?
• Pető Attila (Kreszprofesszor): Az 50-es sebességkorlátozást nem hasraütésszerűen találták ki
• Vargha Márton (Levegő Munkacsoport): M iért legyen 30 km/óra a városi tempó?
• Bereczky Ákos (mikromobilitási szakértő): Észrevesszük-e a szélvédő mögül, hogy élhetetlen a város?
• Bodrog Zoltán (közlekedésmérnök): Ha autósszívatás, akkor legyen tömegközlekedés és P+R parkoló is
• Hetényi László: Magyarország 30 éve Nyugat-Európa gépkocsibontója
• Abelovszky Tamás (Bringaakadémia): Ha egy gyerek nem tud biciklizni a városban, autós lesz belőle
• Balogh Samu (várostervező): A közlekedés megszelídítése érdeksérelemmel jár
• Kunhalmi Zoltán (közlekedésmérnök) - Zéró vízió: új gondolattal behajtani tilos?