Tényleg mindenki hülye matematikából?

A közösségi médiában szélsebesen terjedő változatok száma végtelen – vagy, hogy kicsit nagyképűek legyünk, ∞. A változókat betűk helyett képecskékkel jelölő egyenletrendszerek a legnépszerűbbek. A készítők vélhetően azt feltételezték, hogy az emberek többsége a szabványos matematikafeladatok láttán megijed, és elmenekül a poszttól (valójában azonban, ha van bármiféle csavar a dologban, az a képecskék apró részleteiben rejlik).

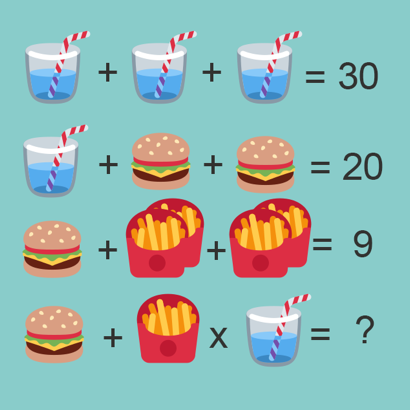
A trükkösnek szánt feladatok kétféle reakciót válthatnak ki az emberekből:

1. Hiába, képtelen vagyok megoldani, még a megoldást sem értem. Idióta vagyok a matekhoz. :(
2. Hogyan lehetnek olyan idióták az emberek, hogy ezt a primitív példát sem képesek megoldani?

Az a reakció azonban gyakorlatilag kizárt (hiába tűnne logikusnak az efféle posztok viralitása láttán), hogy

jaj, de érdekes példa volt, a matematika tényleg szórakoztató tud lenni, végre megértettem, hogy mi szükség van rá az iskolában és a világban.

Az emberek egy részének azért jön ki rossz megoldás például a fenti ábrára, mert az alsó egyenletet balról jobbra próbálja kiszámolni, holott a műveleti sorrend miatt a szorzás magasabb rendűnek számít, így előbb kell elvégezni, mint az összeadást (de itt azért még nem érnek véget a feladatba rejtett csapdák). Nem, nem írjuk le a megoldást. Menni fog az! Ha mégsem, akkor itt egy hosszas magyarázat a Nobel-díjasok heidelbergi fórumának weboldalán, még ennél is sokkal gonoszabb változatokkal. 

Műveleti sorrend

Igazán nagy viharokat azonban mostanában egy másik feladvány keltett a neten, még egyes számológépeknek is beletört a bicskájuk.

A példa mára mémmé vált, hosszas, veszekedésbe fajuló fórumthreadekkel, ellentáborokkal, ahogy azt kell. A problémát a legtöbb ember számára az okozza, hogy a zárójel előtt ott az a kettes. Mivel nincs semmilyen műveleti jel a kettes után, hanem azonnal a zárójel következik, sokan ezeket elválaszthatatlanul összeillőnek gondolják. Így természetesnek tűnik számukra, hogy ezt a műveletet hamarabb kell elvégezni, mint a (fizikailag is) távolabb lévő nyolcas utáni osztást.

Arra szinte mindenki emlékszik az iskolából, hogy mindig a zárójelen belüli műveletekkel kell kezdeni a számolást, vagyis helyesen rájönnek, hogy 2+2=4. Ott vétik a hibát, hogy ezt a négyest rögtön megszorozzák kettővel. Ezután a nyolcat ezzel a nyolccal osztják el, és eredményül egyet kapnak – tévesen.

Ha így írnánk le a feladatot, máris egyszerűbb lenne: 8 ÷ 2 * (2+2) = ?. Pedig semmi mást nem tettünk, mint hogy kiírtuk a kettes után az egyébként is ott lévő szorzásjelet.

Ha esetleg még mindig nem világos, hogy miért, akkor vegyük át a műveleti sorrendre vonatkozó szabályokat. Először a zárójelen belüli dolgokkal kell foglalkozni, aztán a hatványozással, ezután a szorzással és az osztással (amelyek egymással egyenrangúak), végül pedig az összeadással és a kivonással (ezek is egyenrangúak). Az egyenrangú műveleteket pedig balról jobbra oldjuk meg.

Az, hogy vannak kalkulátorok, amelyek eredményül 1-et adnak, nem azt jelenti, hogy több megoldás is helyes lehet, hanem azt, hogy rossz a számológép.

Változó konvenciók

A probléma nem új, más számokkal már korábban is felbukkant. Az amerikaiak számára bonyolítja a helyzetet, hogy korábban az amerikai iskolákban egy betűszóval, a PEMDAS-szal tanították a gyerekeknek a műveleti sorrendet. Ez a betűszó a zárójel, hatványozás, szorzás, osztás, összeadás, kivonás szavak kezdőbetűiből áll össze. A betűk sorrendje alapján sokan (helytelenül) azt feltételezhetik, hogy a szorzás előrébb való az osztásnál, az összeadás pedig a kivonásnál. Pedig nem.

A múlt század elején olyan matematika-tankönyvek is megjelentek, amelyek konkrétan arra tanították a diákokat, hogy először az összes szorzást csinálják meg a kifejezésben, csak ezután álljanak neki az osztásoknak. Továbbá, a matematikai konvenciók is fejlődnek az idővel, így a történelmi korokban

Még egy 1928-as matematikatörténeti mű (A matematikai jelölések története) is azt írta, hogy „azokban a számtani kifejezésekben, amelyekben ÷ és × is szerepel, jelenleg nincs megegyezés arról, hogy melyik műveletet kellene először elvégezni. De ma már azért van konszenzus: amelyik balról nézve előrébb van.

Ínyenceknek itt egy másik példa, amit Kieran Cheetham, a Liverpooli Egyetem fizikusa ötölt ki:

Fogadjunk, hogy az eddigi okoskodás után már el sem hiszi, pedig a válasz 5! (Tényleg. Elnézést, gonosz vicc volt, de akkor is.)

Többet árt, mint használ

De itt nem is ez a példa az érdekes, hiszen az általa okozott felhördülés legfeljebb a matematikaoktatás elégtelenségére hívhatja fel a figyelmet. Sokkal beszédesebb az, hogy ebből globális jelenség lehet, amelyről a New York Timestól az Indexig cikkek születnek. A matematikusok többsége nem hiába gyűlöli az efféle, alapvetően primitív és csak az emberek szívatását célzó példákat. Ezek szerintük csak arra jók, hogy tovább erősítsék a laikusokban egyébként is rettentően erős képet arról, hogy a matematika csak arra jó, hogy

A szándékosan az olvasók összezavarására készült feladatok láttán (illetve a nem kellően megmagyarázott helyes megfejtés érthetetlensége révén) sokakban megerősödhet az a tévhit, hogy ők képtelenek bármiféle matematikai gondolkodásra. Az első iskolai kudarcok után sokan elkönyvelik magukat matematikából hülyének, és az egész életüket így élik le. Ők ezután már a számok (pláne változók), törtvonalak, egyenlőségjelek láttán visszahőkölnek, és esélyt sem adnak maguknak a megértésre.

Pedig az alapszintű matematikában nem sok szerepe van a tehetségnek. A valóságban az általános és a középiskolában azok a diákok lesznek ötösök matematikából (a tényleges zseniken kívül, de az ő számuk sokkal kevesebb, mint a jeles matekosoké), akik az elején hajlandók voltak odafigyelni és gyakorolni. Aki az elejét ellógta, annak később sokkal könnyebb a tehetségre és a génekre fogni saját kudarcait, és ez önbeteljesítő jóslatként valóban nehézségeket okoz neki a tantárgyi alapkövetelmények teljesítésekor. Aztán később, a jelzáloghitel kamatterheinek reális felmérésekor is.

Pincérek, műszakok

A New York Times által megkérdezett matematikusok szerint egy matematikai példának önmagában tényleg semmi értelme, ezért az oktatásban mindig a való világból származó problémákra kell őket lefordítani. Vagyis szöveges feladattá kell őket alakítani, és így a legtöbb esetben megszűnnek a félreértések és az értelmezési problémák.

Nézzük megint az alapproblémát: 8 ÷ 2(2+2) = ? Ezt a következő szöveges feladat megoldóképletének is lehet tekinteni: adott egy étterem, amelyben összesen nyolc pincér dolgozik, két, egyenlő számú alkalmazottat foglalkoztató műszakban (8 ÷ 2). Minden pincér 2 dolláros órabért kap, amit óránként 2 dollárnyi borravalóval egészítenek ki (2+2). Mennyi pénzt keresnek a pincérek együttesen egy óra alatt?

Azt azért ne gondoljuk, hogy minden szöveges feladat egyszerű. Itt egy példa a jó matematikafeladványokra. Ebben nem kell összeadni, szorozni semmit, még csak konvenciókat sem kell követni. A feladvány a szingapúri matematikai diákolimpia egyik feladata volt, és a neten „Cheryl szülinapja” néven vált ismertté. Szingapúrról azt kell tudni, hogy rendszeresen a diákok matematikatudását illető ranglisták élmezőnyében végez. A miniszterelnök, Lee Hsien Loong civilben Cambridge-ben végzett matematikus, és pár éve a saját maga által C++ nyelven írt szúdokumegoldó programjával menőzött a neten.

A kerettörténet szerint Cheryl születésnapja a következő napok egyikén van: május 15., 16., 19., június 17., 18., július 14., 16., illetve augusztus 14., 15., 17. Cheryl elmondja Albertnek, hogy melyik hónapban van a születésnapja (de a napot nem), míg Bernardnak a napot mondja el (de a hónapot nem). Albert ezután így szól: „Én nem tudom, hogy mikor van Cheryl születésnapja, de azt tudom, hogy Bernard se tudja.” Erre Bernard felkiált: „Először valóban nem tudtam, de most már tudom!”. Ezután Albert is megvilágosodik: „Na, most már én is tudom.” A kérdés természetesen az, hogy mikor van Cheryl születésnapja.

Megoldás és levezetés itt, de inkább adjanak maguknak egy esélyt.