Magyar kutatók bizonyították a heavy metal grafén szuperségét

A matematika topológia nevű területe a négy évvel ezelőtti fizikai Nobel-díj óta viszonylag közismertté vált. A topológia az alakzatoknak a folytonos (vagyis szakítás, lyukasztás, ilyesmi nélküli) deformációk - vagyis például nyújtások, csavarások - közben is megmaradó (invariáns) tulajdonságaival foglalkozik.

A sokszor idézett példa szerint egy pogácsa, egy fánk és egy perec a topológia szempontjából egy dologban tér el: abban, hogy hány lyuk van bennük. A topológia azt kutatja, milyen hatások kellenek ahhoz, hogy ez a tulajdonság (nulla lyuk, egy lyuk, két lyuk) egy egész számmal megváltozzon.

A topológiának a pékségen kívül is van alapkutatási és gyakorlati jelentősége is. Egyes kristályokban az elektronok mozgása is topológiai tulajdonságokkal van felruházva, amely alapvető hatással van a fizikai tulajdonságaikra. Ezen keresztül pedig

Hogy közelítsünk a grafén felé: ismert, hogy a grafén egy atomnyi vastag, méhsejtrácsszerűen rendeződő, hat szénatom alkotta gyűrűkből épül fel (gyakorlatilag a grafit egy rétege). A grafént számos okból kutatják, de egy teljes tudományterület születéséhez járult hozzá, amikor kiderült róla, hogy topologikus szigetelőként is működik. Sajnos ahhoz, hogy a veszteségmentes elektromos vezetést megtapasztaljuk a grafén esetében, azt hihetetlenül alacsony hőmérsékletre, az abszolút zéró hőmérséklet közelébe, kellene hűteni. Ez nem egyszerű.

Nehézfémek Brazíliából

Ezután indult be a hasonló, kétdimenziós anyagok utáni kutatás, amelyek hasonló topologikus szigetelőként is működhetnek, viszont jóval magasabb hőmérsékleten. Nemes-Incze Péter MFA-ban működő Topológia Nanoszerkezetekben Lendület-csoportja megmutatta, hogy sokat segít, ha a grafén méhsejtrácsban nem szén tartózkodik, hanem nehézfémek. A kutatók egy ilyen, nehézfémekből álló kétdimenziós kristályról, a jacutingaitról mutatták ki hogy akár szobahőmérsékleten is képes lenne a veszteségmentes elektromos vezetésre.

A platinát, higanyt és szelént tartalmazó ásvány (Pt₂HgSe₃) nevét arról a brazil városról, illetve a mellette lévő aranybányáról kapta (Jacutinga), ahol először megtalálták úgy tíz évvel ezelőtt. Alig néhány mikrométeres szemcsére leltek belőle egy másik ásványban. Azóta már mesterségesen is elő tudják állítani, ilyet vizsgáltak a magyar kutatók is.

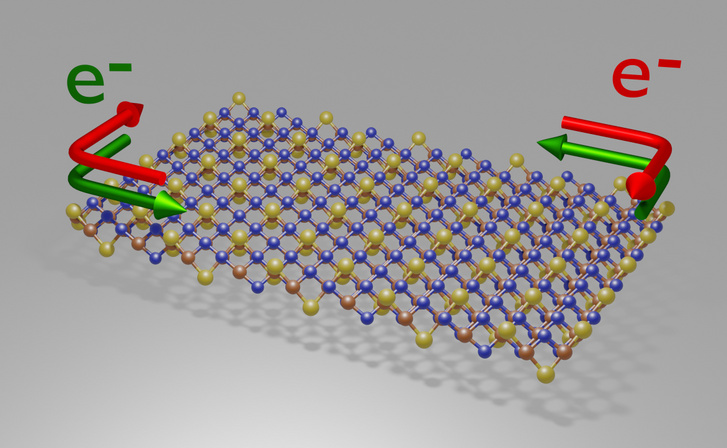
A topologikus szigetelő tulajdonság következménye az, hogy az anyag szélein (ha az atomréteget egy papírlapként képzeljük el, akkor ennek élei mentén) elektromosan vezető csatornák jönnek létre, míg a kristályrács belsejében szigetelő marad. De a vezetésük még ennél is érdekesebb, mert úgymond matematikailag van megtiltva, hogy a széleken haladó elektronok visszaszóródjanak. Így az elektromos ellenállásuk független a vezető hosszától

- mondta el az Indexnek Nemes-Incze Péter. Egy sima vezetőben, ahogy az elektronok haladnak, időnként nekiütköznek az atomoknak, és visszaszóródnak (mondjuk visszapattannak) róluk - ez az ellenállás forrása. Minél hosszabb a vezető, annál több elektron fog visszaszóródni, és csökken az áramerősség.

A topologikus szigetelők szélein - tök triviális matematikai okból, amelyet olvasóink bizonyára jól ismernek, így most nem untatjuk önöket ezzel - viszont veszteségmentesen folyhatnak az elektronok. Mindegy, hogy milyen hosszú a vezető, az áramveszteség nem függ a hossztól. Ez már majdnem olyan jó, mint a szupravezetés, de

A jacutingaitról néhány évvel ezelőtt, elméleti számítások alapján már azt valószínűsítették, hogy a grafénhoz hasonló topologikus szigetelő tulajdonságokkal bír, de ezt eddig kísérletesen senki sem bizonyította. Nemes-Incze Péter és munkatársai a pásztázó alagútmikroszkóp segítségével tapogatták le a jacutingait elektromos tulajdonságait.

Szupravezetés szobahőmérsékleten

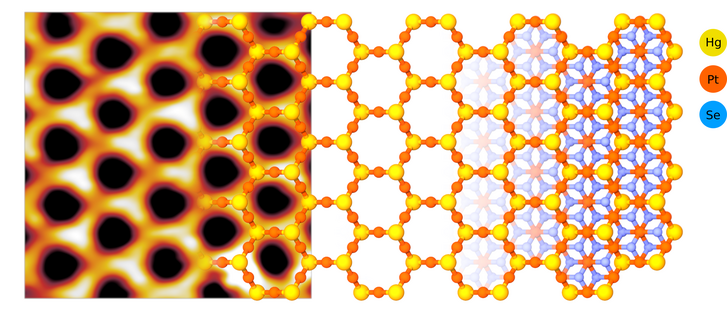
A pásztázó alagútmikroszkóp nagyon vékony tűjét gyakorlatilag minden egyes atom fölé lehet állítani, és rajta keresztül elektronokat lehet juttatni az anyagba. Így ki lehet mérni, hogy a kristályrács különböző pozícióiban milyen a vezetőképesség, és tapasztalható-e elektron-visszaszóródás.

Amikor az elektron áramlása megakad valamilyen kristályrácshibában, és visszaszóródik, a szembejövő elektronokkal interferál, és ezt az interferenciaképet rögzíteni tudjuk a mikroszkóppal. Pontosabban rögzíteni tudnánk, ha a jacutingaitban lenne ilyen hullámzás. De nincs. Az interferencia hiánya pedig bizonyítja, hogy a kristály topologikus szigetelő. Jelenleg nem ismerünk más, nehézfémeket tartalmazó, kétdimenziós kristályrácsot, amely hasonló topologikus vezetési tulajdonságokkal és kémiai stabilitással rendelkezne

- érvel Nemes-Incze. Nem túl nehéz belátni, hogy egy szobahőmérsékleten, az elektromos áramot veszteségmentesen vezető anyagot rengeteg területen lehetne hasznosítani, főként az elektronikában. A jelenlegi számítógépek processzorai azért melegszenek, mert a bennük lévő rengeteg vezetékben áramló elektronok folyton ellenállásba ütköznek.

Ha képesek lennénk egy veszteség nélküli vezetőből számítógép-alkatrészeket gyártani, az áttörést jelentene a számítástechnikában. Ahogy a topologikus szigetelőket kettévágjuk, a matematikai szükségszerűségek miatt a létrejövő két darab élei mentén megint csak veszteségmentes vezetőállapot jön létre. Vagyis elméletileg a kristály darabolásával vezetékeket lehetne gyártani.

A jelenleg fejlesztett kvantumszámítógépek mindegyike azzal a problémával küszködik, hogy a számítások elvégzéséhez szükséges kvantumállapot csak pillanatokig tartható fenn. Így minden számítást e rövid idő alatt kell elvégezni, mielőtt a qubitekben tárolt információ elveszne. A topologikus vezetők segítségével e probléma kiküszöbölhető lehetne, hiszen a kristályszerkezet normális körülmények között is különleges kvantumtulajdonságokkal bír.

A topologikus kvantumszámítógépet célzó elméleti kutatásokat már most tolja a Microsoft, és a fejlesztés már azelőtt átkerült az alkalmazás térfelére, mielőtt egyáltalán bizonyíthatták volna, hogy a tervek megvalósíthatók a gyakorlatban is.