Bepillantottak tudósok a negyedik dimenzióba

Két különálló tudóscsoport – egy amerikai és egy európai – is olyan, hasonló kísérleti eredményeket mutatott be a Nature tudományos lapban, amik alapján azt állítják, hogy a mi háromdimenziós térbeli világunkban is ki lehet mutatni a negyedik térbeli dimenzió hatását.

A jelentős áttörésként is értékelhető kutatási eredmények elég régi tudományos problémakörbe hozhatnak újdonságot. Azt ugyanis elég régóta feltételezik matematikusok, fizikusok és a határtudományok képviselői, hogy az általunk ismert és lakott három térbeli dimenzión kívül létezhetnek, léteznek további térbeli dimenziók (az időt mint dimenziót nem ide sorolva). A gond ezzel eddig az volt, hogy miképp egy síkban élő, kétdimenziós teoretikus élőlénynek sincs könnyű dolga megismerni, megtapasztalni a háromdimenziós világot, úgy a háromdimenziós térben élő ember se tudott idáig érdemben megismerkedni a feltételezések szerint igenis létező, magasabb szintű, többdimenziós terekkel.*

Ebbe a helyzetbe hoz radikális változást a két most közzétett tanulmány, és mivel egymástól függetlenül dolgozó kutatókról van szó, eredményeik egymást erősítik. Sajnos nem arról van egyelőre szó, hogy megtalálták volna a titkos átjárót a negyedik dimenzióba, és hamarosan ki-be járkálhatunk majd a terekbe tetszésünk szerint, vagy akár utazhatunk is az időben. Annyi történt, hogy

azaz túlléptek azon, hogy a negyedik dimenziós teóriákra eddig csak elméleti, matematikai bizonyítékok léteztek (azaz kockát tudunk gyártani, de négydimenziós hiperkockát egyelőre nem).

A két kutatócsapat két különböző, de némileg hasonló módon jutott ugyanarra az eredményre. A fizikusok kétdimenziós rendszereket állítottak fel, az egyik csapat ultrahideg atomokból, a másik fényrészecskékből. Kísérleteik eredményei eltérőek voltak, de kiegészítették egymást úgy, hogy amit láttak, az felfogható a negyedik dimenzióban észlelt kvantumos Hall-effektusnak.

A kvantált Hall-jelenséget Klaus von Klitzing fedezte fel 1980-ban, rá öt évvel felfedezését Nobel-díjjal jutalmazták. A lényege röviden: ha egy síkszerű elektromos vezetőben a síkra merőleges mágneses tér jelenlétében áram folyik, akkor a vezető két oldala között az elektronokra ható Lorentz-erő miatt feszültség jelenik meg. Ez a Hall-effektus. Ennek speciális formája, hogy kvantumosan, azaz nagy tisztaságú kétdimenziós elektrongázban és elegendően nagy mágneses térben vizsgálva meglepő viselkedés tapasztalható: a Hall-ellenállás nem egyenletesen, hanem lépcsőszerűen változik, miközben a longitudinális ellenállás nulla értéket vesz fel a "lépcsők" vízszintes részein. A kvantumos Hall-effektus központi kérdésköre: a kétdimenziós felületen csapdába eső elektronok tulajdonságainak változása mágneses tér hatására egész számok többszöröseivel írható le. A matematika szerint ebből az következik, hogy a jelenség négydimenziós térben is mérhető lenne – csakhogy fizikailag nincs hozzáférésünk ehhez a térhez.

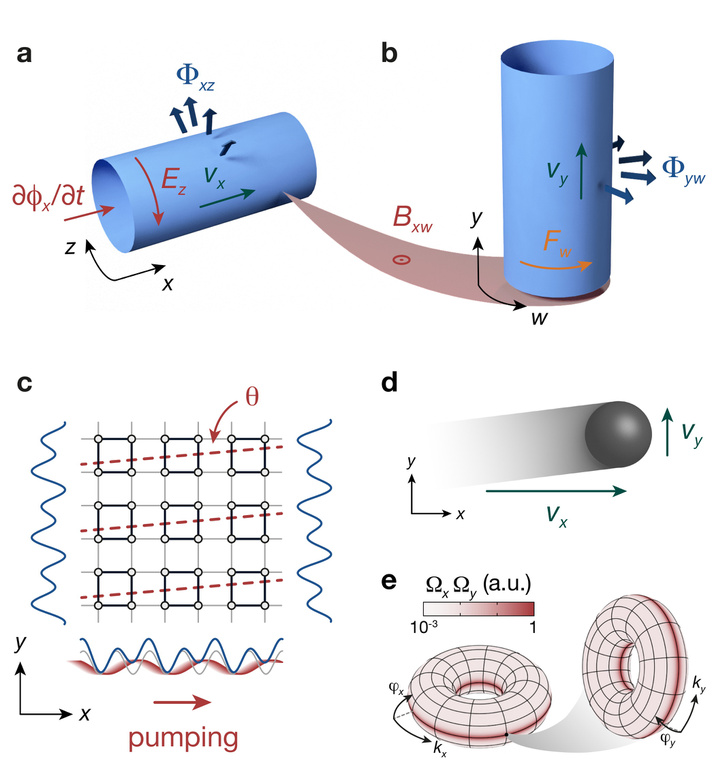
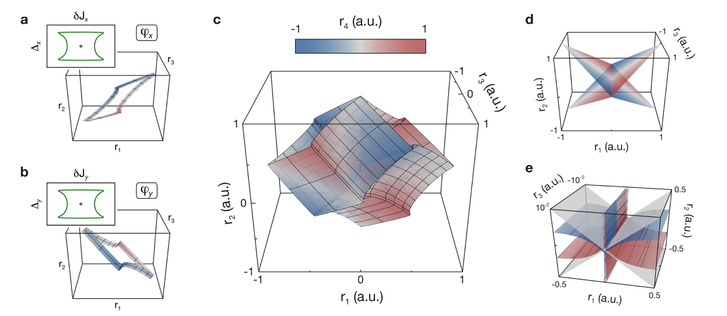
Mindkét kutatócsapat sikerrel kerülte meg ezt a akadályt az általuk kifejlesztett kísérleti rendszerekkel. Az európai fizikusok rubídiumatomokat ejtettek síkbeli csapdába lézerekkel (az eredményt kb. úgy kell ezt elképzelni, mint egy tálca tojást), ezzel létrehozva egyfajta kétdimenziós kvantumos töltéspumpát, amivel elektromos töltések mozgását tudták szimulálni az amúgy semleges töltésű atomokon. Mindehhez egy ráadás paramétert társítottak, az egyes atomok mátrixban elfoglalt pozíciója alapján, ezzel két további térbeli dimenziót szimulálva. Mindezzel képesek voltak megmérni az úgynevezett második Chern-számot, ami a negyedik dimenzióban zajló hatások jelenlétét jelezte. (A Chern-osztály bonyolult vektoros rendszerek leírására szolgáló állandók sora a geometrikus algebrában.) Az európai tudósok tanulmánya itt olvasható: .pdf.

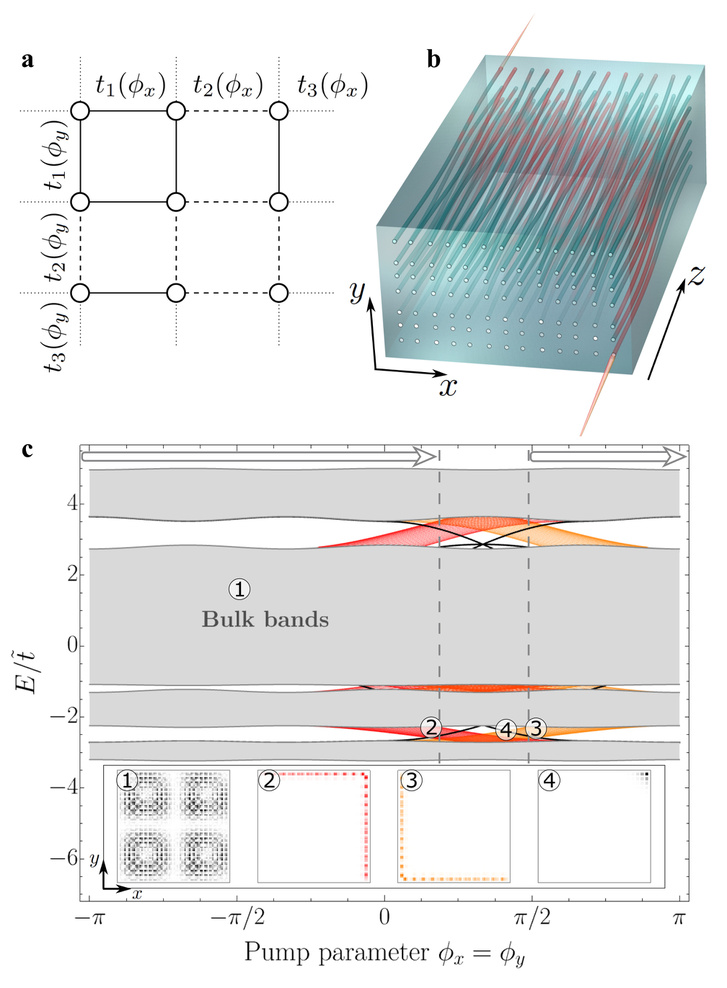
Az amerikai csapat speciális üvegen keresztülhaladó fény viselkedését tanulmányozta (tanulmányuk: .pdf). A különleges, szálakból alkotott üveg afféle hullámvezetőként képes volt a fényhullámok alakját szabályozni. Az üvegszálköteg csavarásával a töltött részecskék elektromos mezejének viselkedését tudták szimulálni, csak itt fotonok (töltés nélküli fényrészecskék) játszották mondjuk az elektronok szerepét. Eközben azt tapasztalták, hogy a fotonok az “üvegkalitka” ellentétes élei és sarkai közt ugráltak, ez pedig állításuk szerint a 4D-s kvantum Hall-effektus 3D-s fizikai hatása.

A most elvégzett két kísérletsorozat fontos alapvető tudományos kiegészítésekkel szolgálhat, sőt, általa

Az eredményeiket úgy érdemes elképzelni, hogy a már említett teoretikus kétdimenziós élőlény alkothat némi fogalmat arról, hogyan nézhet ki egy háromdimenziós objektum, ha megfigyeli annak kétdimenziós árnyékát. Ugyanígy mi is tanulhatunk a negyedi dimenzió természetéről, ha megfigyeljük az ottani objektumok, jelenségek “árnyékát” a mi világunk fizikai rendszereiben.

“Fizikai értelemben nincs 4D-s térbeli rendszerünk, de hozzáférhetünk 4D-s kvantumos Hall-fizikához ezekkel a az alacsonyabb dimenziójú rendszerekkel, mivel a magasabb dimenziójú rendszerek kódja megjelenik a vizsgált struktúrák bonyolultságában” – magyarázta Mikael Rechtsman a Penn State University professzora a Gizmodonak. “Egyszer talán képesek leszünk előállni a magasabb dimenziók új fizikájával, és aztán olyan eszközöket tervezni, amik kihasználják a magasabb dimenziójú fizikát az alacsonyabb dimenziókban.”

*Arról, hogy a különböző 2- 3- és 4-dimenziós világok hogyan viszonyulnak egymáshoz, a Gizmodo ásott elő egy elég szemléletes videót:

Nyitó illusztráció: Samsung Hypercube egy angliai zenei fesztiválon (Matt Cardy/Getty Images Hungary)