Bizonyították Erdős Pál 80 éves sejtését
További Tudomány cikkek
-
Vészhelyzeti csúcstalálkozót hívtak össze a kutatók, katasztrofális tengerszint-emelkedésre figyelmeztetnek - Kiderült, az állva végzett irodai munka semmivel sem egészségesebb, mint ha ülve dolgozunk
- Horror vagy médiahack az első fejátültetés?
- És ön mennyit káromkodik a munkahelyén?
- Vulkánkitörések alakíthatták a Hold túloldalát
Erdős Pál
Valószínűleg sikerült megoldani Erdős Pál több mint nyolcvan éve felvetett sejtését, amelyért még anno 500 dolláros díjat tűzött ki maga a matematikus. A probléma, hogy a számítógéppel végzett bizonyítás olyan bonyolult, hogy ember soha nem tudja ellenőrizni.
Alexei Lisitsa és Boris Konev, a Liverpool Egyetem két kutatója az, aki elérte az áttörést. Mielőtt megvizsgálnánk az ő bizonyításukat, nézzük, miről is szól Erdős Pál elmélete.
Erdős elmélete
Maga az elmélet sem egyszerű, de több lépésben meg lehet magyarázni ennek a blognak a segítségével. Tegyük fel, hogy alma- és narancsfákat ültetünk egymás után sorban. Az első fánál elindulva összeszámoljuk, mennyi alma és mennyi narancsfát látunk, a számot fel is jegyezzük a papírra. Hogy könnyebb legyen utána dolgozni a számokkal, ha az almafák számolásánál narancsfára bukkanunk, akkor az almafák eddigi számát írjuk fel.
Hat fából álló sor esetén ez így néz ki:
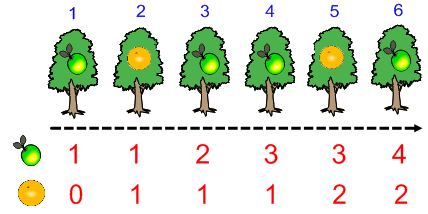
Almasor: 1 1 2 3 3 4 (vagyis egy alma, egy narancs, második alma, harmadik alma, narancsfa - így marad három alma, negyedik alma)
Narancssor: 0 1 1 1 2 2 (egy alma - tehát nulla narancs, egy narancs, marad az egy narancs, marad az egy narancs, második narancs, marad a két narancs)
Most vonjuk ki egymásból az almafák és narancsfák közötti különbséget és a következő számsort kapjuk:
1 0 1 2 1 2
Amit keresünk, az a kétféle gyümölcsfa közötti legnagyobb eltérés, és ez a 2.
Az első feladat: hogyan tudjuk úgy ültetni a fákat, hogy a legnagyobb eltérés 1 legyen?
Most nézzünk egy másik feladatot: nem mindegyik fát számoljuk meg, hanem csak minden másodikat vagy harmadikat vagy negyediket, és így tovább. Ezt nevezzük kihagyásos számolásnak.
A példában vegyünk például minden második fát, így a sorozat a következőképpen alakul:
Almasor: - 0 - 1 - 2
Narancssor: - 1 - 1 - 1
A kettő különbsége:
- 1 - 0 - 1
A legnagyobb különbség most 1, ezt nevezzük eltérésnek (discrepancy). És el is érkeztünk a következő feladathoz.
Ültess úgy egy 11 fából álló sort, ahol bármelyik kihagyásos számolást használunk, a legnagyobb eltérés 1. Bármilyen részsorozatot használhatunk erre, a lényeg, hogy az eltérés mindig 0 vagy 1 legyen.
Ha ez megvan, akkor azt kell bebizonyítani, hogy az előző feladat nem megoldható 12 fával.
Vagyis, ha azt akarjuk, hogy az eltérés ne legyen nagyobb 1-nél, akkor meg kell állni a fák ültetésével valahol.
Mi a helyzet akkor, ha azt szeretnénk, hogy az eltérés ne legyen nagyobb 2-nél? A sejtések szerint 1124-nél kell megállni, de ezt még nincs bizonyítva. Ugyanúgy meg lehetne nézni a 3, 4, 5, stb. legnagyobb eltéréseket. A matematikusok eddig nem tudták bebizonyítani, de úgy gondolják, hogy ezeknél is van egy felső határa az ültetett fáknak.
És el is érkeztünk Erdős Pál tételéhez, amely azt mondja, hogy
Akármekkora eltérést veszünk, mindig van egy felső határa a fák (elemek) számának a sorozatban.
13 gigás bizonyítás
Alexei Lisitsa és Boris Konev bebizonyította, hogy a végtelen sorozatoknál biztosan nagyobb az eltérés 2-nél. Egy 1161 számból álló sorozatot vizsgáltak meg számítógéppel, és a kapott adatok 13 gigabájtos fájt adtak ki. Ez nagyobb, mint a 10 gigabájtosra becsült teljes (tömörítve letölthető) Wikipedia-anyag. A kutatók által írt program több mint hat órán át dolgozott. Valószínűleg ez a leghosszabb bizonyítás, ami matematikai tételre valaha is készült.
A kutatók elismerték, hogy a számítógépes bizonyítás az emberi teljesítőképességen túl van. De egyelőre nincs jobb megoldása a problémának. Ez persze nem jelenti azt, hogy nem is lehet a jövőben.
A matematikusok egyébként nincsenek ellene a számítógépek felhasználásának. Matt Parker, a University of London matematikusa úgy fogalmazott, hogy a számítógép emelte a tétet, de az emberi kreativitás az, amely ezt lehetővé tette. Chris Budd, a Royal Institution of Great Britain matematikusa a számítógépek megjelenését a matematikában a nyomtatás megjelenéséhez hasonlította, amely végtelen lehetőségek előtt nyitja meg az utat.
Kövesse az Indexet Facebookon is!
Követem!
