A Gömböctől az űrbéli krumpliformákig

2007 elején a világsajtó felkapott egy furcsa, teknőspáncélszerű idomot, aminek készítői a Gömböc nevet adták. Az idom eredetileg a matematikai formát leíró tanulmányt közlő neves szakfolyóirat, a Mathematical Intelligencer borítóján jelent meg, aztán a Gömböc hódító útra indult a Scientific Americantól a Daily Telegraphig, egyik példánya pedig a Cambridge-i Egyetem tudománytörténeti múzeumának állandó kiállítási tárgya lett.

Mi is az elsők között adtunk hírt a „matematikai őssejtről”. A tanulmány egyik szerzője, dr. Domokos Gábor, a BME Szilárdságtani és Tartószerkezeti Tanszék professzora nevezte így Gömböcöt, utalva arra, hogy olyan homogén testről van szó, aminek csupán egyetlen stabil és egyetlen instabil egyensúlyi helyzete van. Korábban csak sejtették, hogy létezik ilyen keljfeljancsi, Domokos és kollégája, Várkonyi Péter igazolták ezt a sejtést.

A két kutató a tanszék egy harmadik munkatársával, Sipos András Árpáddal, valamint Szabó Gyulával együtt nemrég újabb neves szaklapban, az Astrophysical Journalben közölt cikket. (Szabó az SZTE tanársegédje, jelenleg a Lendület Fiatal Kutatói Program keretében az MTA Csillagászai Kutatóintézetében dolgozik tudományos munkatársként.) A cikk ezúttal aszimmetrikus testekről szól, nevezetesen az űrben keringő aszteroidákról, azt pedig egy óvodás is tudja, hogy ezeknek szabálytalan a formájuk, mint egy krumplié. Na de miért pont olyan? Miért nem gömb alakúak a kisbolygók?

Fénypontból geometriai modell

Az utóbbi években több aszteroida alakját megismertük, nyolc kisbolygón szonda is landolt. Nagyfelbontású képek, radarmegfigyelések is készültek, mégis keveset tudunk a kisbolygók formájáról – például csak körülbelül százhoz létezik fotometriai modell.

A fotometria a csillagászat egyik legfontosabb eszköze, ami az égitestek fényességváltozását elemzi, ebből következik a fotometriai modell magyarázata is. „A kisbolygók fényességintenzitásában bekövetkező változásokat figyeljük különböző rálátási szögeknél és pozícióknál. Ha elég sok – általában évtizedekig visszamenő – megfigyelés gyűlik össze, elég jól meg tudjuk határozni egy aszteroida alakját” – fogalmaz Szabó Gyula.

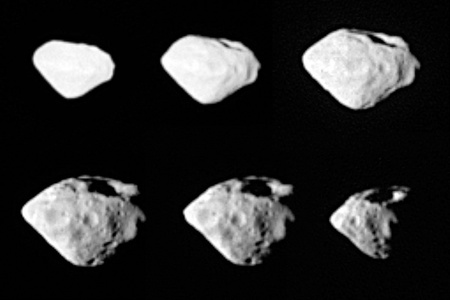
A fényességváltozások alapján igen bonyolult, sok ismeretlent – például az aszteroida forgástengelyének helyzetét – tartalmazó képletekkel számolják ki a fotometriai modellt. Körülményes munka, de nem nagyon van jelenleg jobb módszer: a legjobb távcsövek is pontszerűen látják majdnem az összes kisbolygót, és nem küldhetünk mindegyikhez űrszondát. Az említett száz modell mögött tehát rengeteg meló van, a számolásokon túl az utóbbi harminc-negyven év kisbolygó-megfigyelési eredményei.

Ezen eredmények eléggé változatos formákról tanúskodnak: léteznek nem konvex, azaz homorú felülettel is rendelkező kisbolygók, kettéágazó objektumok és dióformák is, de feltűnően sok aszteroidán találni nagy lapos felületeket és határozott éleket – a nagyfelbontású képek szerint a kis aszteroidák legalább fele ilyen. Domokosék arra voltak kíváncsiak, miként alakulhattak ki ezek a lapos-éles űrkrumplik.

Koptatott krumpli

Keveset tudunk arról, hogy az idő során hogyan és milyen fizikai folyamatok révén formálódnak az aszteroidák, de a kutatók azt feltételezték, hogy a parányi porszemek, mikrometeorok markáns alakformáló erőt képviselnek. Ezekből az apró objektumokból ugyanis rengeteg található az űrben, és mivel a kisbolygóknak nincs légkörük, a mikrometeorokat semmi nem akadályozza meg abban, hogy becsapódjanak. És bármilyen kicsi is legyen egy ilyen becsapódás, sok van belőle.

E mikroütközések alapján Domokosék készítettek egy átlagoló kopási modellt, ami azon a feltételezésen alapul, hogy az aszteroidákat folyamatosan bombázó, nagy sebességű mikrometeorok véletlenszerű irányúak, vagyis bármelyik irányból ugyanolyan valószínűséggel érkezhetnek. A korábbi elméletek szerint a kis becsapódások tompítják az éles éleket, a magyar tudósok tanulmánya azonban arra vezetett rá, hogy éppen ezek a mikroütközések törik meg az O(3) szimmetriát.

E szimmetria nevezetes fogalom a geometriában, és a példánkra vonatkoztatva nagyjából annyit jelent, hogy ha a térben egy testet minden irányból egyformán koptatok, joggal várhatnám azt, hogy abból előbb-utóbb gömb lesz. De az űrben ez mégsem alakul így, hiszen nem nagyon találni gömb alakú aszteroidákat. Ennek oka pedig a kopás jellege: a mikrometeorok kis részeket pattintanak ki az aszteroidákból, amik vagy megszöknek, vagy az aszteroida saját gravitációja megfogja őket.

Domokos és kollégái elkészítették modelljük finomított változatát is, ami figyelembe veszi a kipattintott anyag visszahullását a kisbolygó felszínére. E modell alapján az aszteroidák nem szabályos alakzatokká formálódtak, hanem nagy és viszonylag lapos területekkel, határozott élekkel rendelkező, krumpliszerű objektumokká – éppen olyan aszteroidákká, amiből rengeteg kering odakint.

„Mondok egy analógiát az élek szükségszerű kialakulására” – magyarázza Domokos. „Tegyük fel, hogy van egy nem kör alakú, de sima kontúrral rendelkező (például ellipszis alakú), gyúlékony területem. Ennek felgyújtom a szélét, és szélcsend van, tehát minden irányban egyenletesen terjednek a lángok a terület belseje felé. A még le nem égett belső rész kontúrja nem körhöz fog közelíteni, előbb-utóbb valahol ki fog alakulni egy csúcs. (A préritüzek vizsgálatánál ismert ez jelenség, a tüzek elméleti „csontvázát” is gyakran meghatározzák ez alapján.)”

Valahogy így sérül az O(3) szimmetria az aszteroidáknál is: a kezdőforma tökéletlenségét nem lecsiszolják, sőt éppen hogy felnagyítják a kis becsapódások, és előbb-utóbb valahol kialakul egy él. A kutatók felismerésének lényege, hogy a gömb ebben a folyamatban nem vonzó, hanem taszító forma.

Hozzá kell tenni azonban, hogy ez nem igaz minden kopástípusra. A mikrobecsapódások esetében működik a fenti modell, de létezik olyan kopás, ami tökéletlen formából létrehozza a gömböt. Ilyen például, amikor egy kavics görög a folyóágyon, ez ugyanis egészen más fizikai folyamat, mint az aszteroidák kopása. „Ebben az esetben a koptató testek jellemzően nagyok, és más modell szerint alakítják a kavics formáját, közel gömbszerűvé” – magyarázza Domokos.

Miről árulkodnak a kavicsok?

A kopási modell még sok tényezőt nem vesz figyelembe, például a nagyobb tárgyakkal való ütközést és a kráterek keletkezését – pontos mennyiségi becsléseket tehát még nem lehet levonni a modell alapján. A kutatás jelentősége inkább abban áll, hogy felhívja a figyelmet a mikroütközések dominanciájára a kopási folyamatokban. A modellből egyébként egészen jól meg lehet jósolni egy aszteroida további kopását, és a kiindulási formára is lehet következtetéseket levonni, de csak korlátozottan.

De persze nem minden kisbolygóra alkalmazhatók a fentiek. Minél nagyobb egy aszteroida, annál jellemzőbb, hogy nála kisebb testekkel ütközik – létezhet olyan tartomány, ahol nem a mikroütközések uralják a kopást.

És hogy mire jó, ha ismerjük az aszteroidák alakját és formálódási folyamatát? A formai jellegzetességek és a kisbolygók kora között vannak összefüggések, így az alakból arra is lehet következtetni, hogy milyen régi az aszteroida. A fotometriai modellből pedig megtudható egy aszteroida forgástengelye is. „Körülbelül kétszázezer kisbolygót ismerünk, és azt sejtjük, hogy ezek kialakulásában a becsapódások kulcsszerepet játszanak” – magyarázza Szabó.

„Van tehát kétszázezer próbatestünk mindenféle méretben – rendkívül sok információval szolgál, ha ezeket megfigyeljük. Az ütközési folyamatokból pedig végső soron nemcsak a kisbolygók kialakulására lehet következtetni. Más naprendszerek kialakulására, üstökösszerű, esetleg bolygó méretű objektumok létrejöttére is választ lehet kapni.”

Szabónak bizonyára nem ez az utolsó kutatása a témában – tavaly is publikált már cikket a kisbolygók alakjának formálódásáról –, de a BME-sek egyelőre visszaszálltak a földre. Az ötödéves hallgató Szabó Tímeával kibővült csapat a már említett folyami kavicsokkal foglalkozik, azzal, hogy az alakjukból mennyire lehet következtetni a kavicsokat kialakító fizikai folyamatokra. Ez a kutatás még közelebb áll a Gömböchöz, mert míg általában a geológiában a kavicsokat három önkényesen meghatározott tengely irányában mért átmérőjükkel írják le, Domokosék abból indulnak ki, hogy az egyes kavicsok hány egyensúlyi helyzettel rendelkeznek.

„Rengeteg következtetést lehet ebből levonni, például bizonyos anyagú kavicsok kristályszerkezetük miatt jellegzetes formákká töredeznek, ezek pedig jellemző egyensúlyi helyzetekkel járnak” – fogalmaz a professzor. Ezekből a speciális formákból tehát akár a kavics anyagát is meg lehet mondani.

Az alaktani kutatásoknak azonban egy esztétikai, sőt filozófiai vetülete is van. „A Gömböcöt sok ember szépnek tartja, pedig léteznek nála lágyabb formák. Érdekel bennünket az is, miért tartunk szépnek egy olyan markáns élt, mint amilyen a Gömböcnek van” – mondja Domokos. „Ennek lehetnek természeti analógiái, és a válasz azokban a folyamatokban van, amelyek létrehozzák ezeket a formákat.”